2630번: 색종이 만들기
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다.
www.acmicpc.net



문제
아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.

전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.
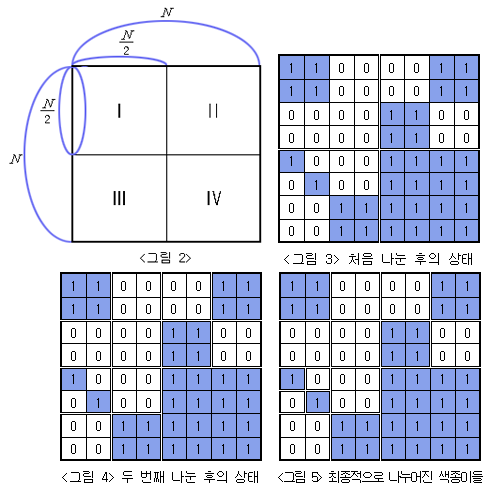
전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.
입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.
출력
첫째 줄에는 잘라진 햐얀색 색종이의 개수를 출력하고, 둘째 줄에는 파란색 색종이의 개수를 출력한다.
<<소스코드>>
import sys
n = int(sys.stdin.readline()) #전체 종이의 한 변의 길이
paper = [list(map(int,sys.stdin.readline().split())) for _ in range(n)] #입력값 paper라는 리스트에 추가
white = 0 # 하얀색 카운트 = 출력값
blue = 0 # 파란색 카운트 = 출력값
def check_paper(x,y,n): #재귀함수 생성,x와 y는 좌표, n은 종이 길이
global white,blue
color_check = paper[x][y] #시작 좌표의 값(예제에서는 1)으로 비교 시작
for i in range(x,x+n):
for j in range(y,y+n):
if color_check != paper[i][j]: #color_check = 1 이므로(예제), paper[i][j]가 1이 아니라면(즉 하나라도 같은 색이 아니면), n을 2로 나누고 4등분 시작
check_paper(x,y,n//2) #좌상단
check_paper(x,y+n//2,n//2) #우상단
check_paper(x+n//2,y,n//2) #좌하단
check_paper(x+n//2,y+n//2,n//2) #우하단
return
if color_check == 1: #만약 모두 1이면, 1은 파란색이므로 전역변수 blue 의 카운트 1 증가
blue += 1
else:
white +=1
check_paper(0,0,n)
print(white)
print(blue)
<<결과값>>
8
1 1 0 0 0 0 1 1
1 1 0 0 0 0 1 1
0 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
1 0 0 0 1 1 1 1
0 1 0 0 1 1 1 1
0 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1
9
7
분할정복(Divide and Conquer)
어떤 문제를 해결하는 알고리즘에서 원래 문제를 성질이 똑같은 여러개의 부분 문제로 나누어 해결하여 원래 문제의 해를 구하는 방식이다.
방법은,
2개 이상의 작은 문제들로 쪼개고(Divide) -> 나누어진 작은 문제를 푼다(Conquer) -> 나누어 해결한 문제들을 합친다(Combine)
대표적인 예로 거듭제곱을 구할 수 있는데, 함수를 통해 for문으로 c^n 값을 구하는데의 시간복잡도는 O(n)이고(n만큼 곱하는 계산을 하기 때문에), 분할정복을 이용하면 O(logn) 이기 때문에 시간복잡도에서 우위를 갖는 알고리즘 방법이다.
쿼드트리
자료 구조의 트리를 기반으로 자식 노드가 4개인 트리. 공간을 재귀적인 호출로 4개의 자식노드로 분할하는 방법. 매우 큰 지형을 빠르게 검색할 수 있다. 해당 문제는 쿼드트리 자료구조 문제였다.
어려운것&배운것
이문제는 스스로 풀 수가 없었다. 답안을 확인해서 처음부터 끝까지 디버깅해보고 겨우 이해해서 안보고 내내 코드/ 내 변수로 바꿔서 처음부터 끝까지 쓸 수 있을때까지 주석 하나하나 달아가며 풀었다.
이걸 생각한 사람들은 천재인가... 덕분에 분할정복/쿼드트리가 무엇인지 알고는 지나갈 수 있겠다.
global 이 전역함수라는 것도 배우고 간다. 기본개념인 것 같은데 이제 알았네! 이제라도 알면 됬다.
재귀함수에서의 매개변수가 조금 헷갈렸다ㅠㅜ 그래서 그림으로 그렸다. 각 시작점을 써놓고 시작하면 양방향 탐색을 이해하는데 도움이 된다!
'알고리즘' 카테고리의 다른 글
| [JS] 프로그래머스 1일 1문제 풀기 - 가운데 글자 가져오기 (0) | 2021.04.24 |
|---|---|
| [파이썬] 단계별 문제 풀기 - 15650번 백트래킹 (N과 M 2) (0) | 2021.03.17 |
| [파이썬] 단계별 백준 문제 풀기 - 2108번 정렬 (통계학) (0) | 2021.03.17 |
| [파이썬] 단계별 백준 문제 풀기 - 1260번 DFS/BFS (DFS와 BFS) (0) | 2021.03.16 |
| [파이썬] 단계별 백준 문제 풀기 - 18258번 큐 (큐 2) (0) | 2021.03.16 |