9461번: 파도반 수열
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의
www.acmicpc.net

문제

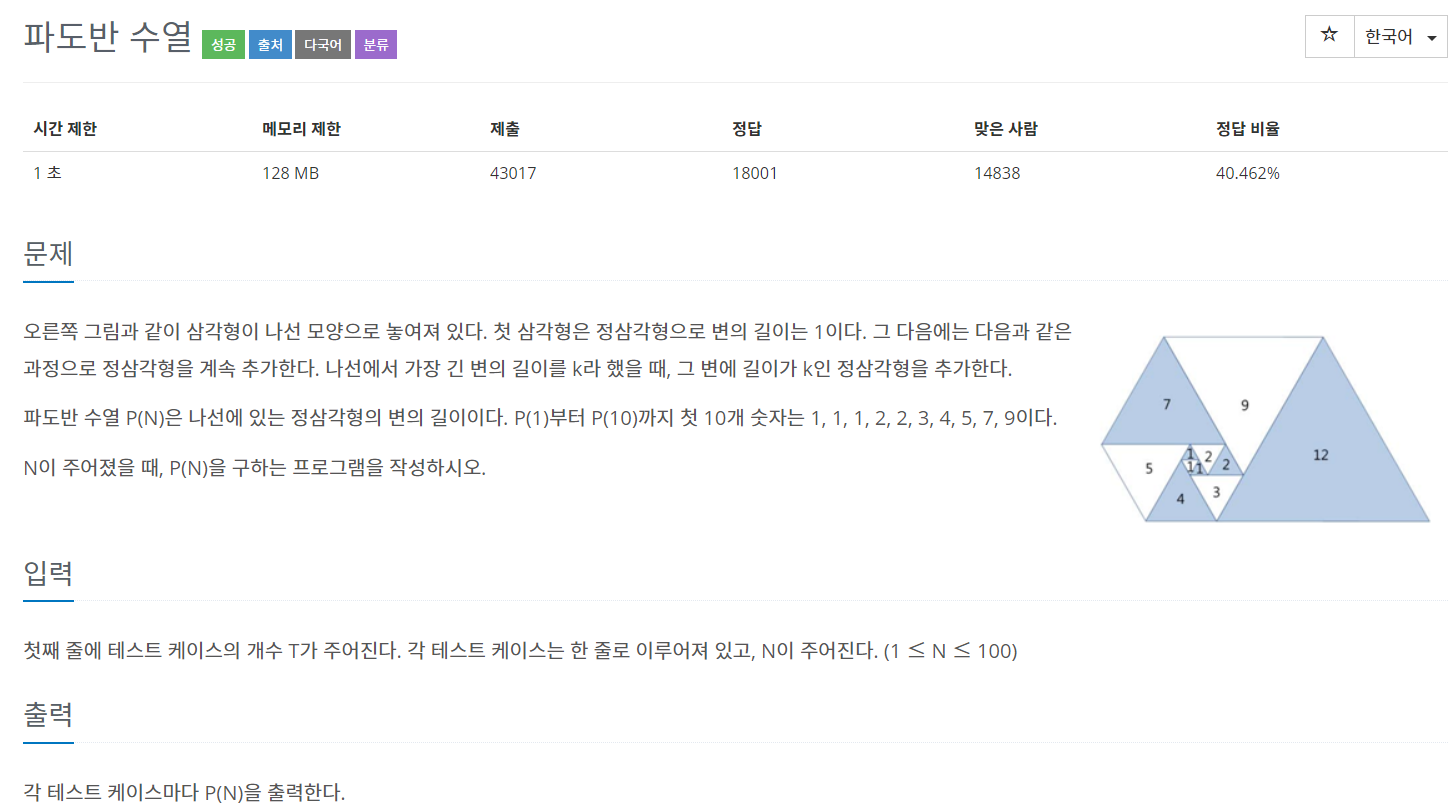
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
<<소스코드>>
tri(n,memo)에서 memo 생략가능
import sys
#메모이제이션, memo를 만들어 1~3의 값을 저장해주었다.
memo = {
1: 1,
2: 1,
3: 1
}
#dp 함수 생성
def tri(n,memo):
if n > 3: #n이 3 이상일 때, memo에 값이 있다면 memo[n]값 반환
if n in memo:
return memo[n]
else: n이 3이하라면 그냥 1 출력
memo[n] = 1
return 1
#수열은 2번째 전, 3번째 전의 값의 합이다! (아래 표 설명)
nth_tri = tri(n-2,memo) + tri(n-3,memo)
memo[n] = nth_tri # nth_tri를 memo[n]에 담아주고 반환해준다
return nth_tri
t = int(sys.stdin.readline()) #테스트케이스 수
for i in range(t):
a = int(sys.stdin.readline()) #입력되는 값
print(tri(a,memo)) #tri 함수 실행<<결과값>>
2
6
3
12
16신나는 함수(백준 9184번)을 방금 풀고 와서 그런가.. 그래도 어렵지 않게 풀 수 있었다.
똑같이 동적계획법(dynamic planning) 문제로, tri라는 함수를 실행해 주었고, P(N) = P(N-2) + P(N-3) 이기 때문에 N을 3 이상으로 잡아주었다. 그 미만은 어차피 다 1이므로 1값을 반환했다.
P(N)의 규칙

즉 P(10) = P(8) + P(7) , 9 = 5+4
P(N) = P(N-2) + P(N-3) 을 쉽게 구해서 풀 수 있는 문제였다.
'알고리즘' 카테고리의 다른 글
| [파이썬] 단계별 백준 문제 풀기 - 1037번 약수 (0) | 2021.03.15 |
|---|---|
| [파이썬] 단계별 백준 문제 풀기 - 1149 동적 계획법 1 (RGB거리) (0) | 2021.03.14 |
| [파이썬] 단계별 백준 문제 풀기 - 9184 동적 계획법 1 (신나는 함수 실행) (0) | 2021.03.13 |
| [파이썬] 단계별 백준 문제 풀기 - 1436 (영화감독 숌) (0) | 2021.03.13 |
| [파이썬] 단계별 백준 문제 풀기 - 4948 기본수학2 (베르트랑 공준) (0) | 2021.03.13 |